深搜与回溯-N皇后问题
问题描述
N皇后问题,即在一个N*N的国际象棋的棋盘上,在不与规则冲突的前提下,求解摆放皇后的方法。其来源于八皇后问题
八皇后问题,是一个古老而著名的问题,是回溯算法的典型例题。该问题是十九世纪著名的数学家高斯1850年提出:在8X8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。 高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。计算机发明后,有多种方法可以解决此问题
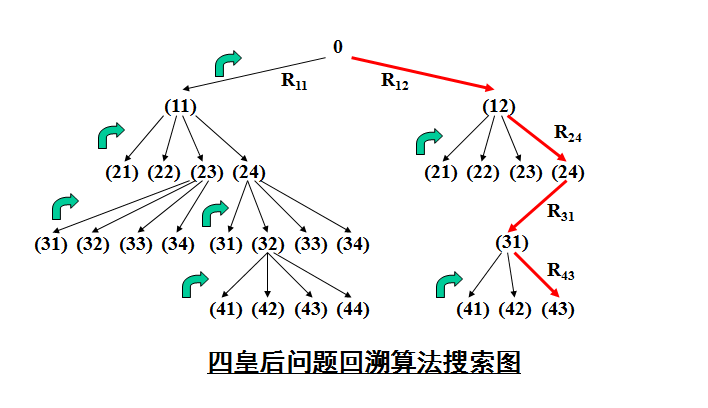
回溯法
1、回溯法,构造一个解,n为30以下可在忍受时间内完成
//n皇后问题
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <stack>
using namespace std;
typedef struct{
int x,y;
}node; //定义棋盘上的点
vector<int> vy,vzuo;
vector<int> vyou; //vy收集已经不能放置皇后的列,vzuo收集已经不能放置皇后的左斜线'/ ',vyou收集已经不能放置的右斜线'\'
stack<node> s,sok; //s栈收集已经放入棋盘的皇后位置
int n;
node a;
bool try_hh(node k) //判断k点的皇后能否放置
{
for(int i=1;i<vy.size();++i)
{
if(k.y==vy[i] || (k.x+k.y)==vzuo[i] || (k.y-k.x)==vyou[i])
return 0;
}
return 1;
}
bool huishu ()
{
node b;
b=s.top();
s.pop();
vector<int>::iterator result=find(vy.begin(),vy.end(),b.y);
if(result!=vy.end())
vy.erase(result);
result=find(vzuo.begin(),vzuo.end(),(b.x+b.y));
if(result!=vzuo.end())
vzuo.erase(result);
result=find(vyou.begin(),vyou.end(),(b.y-b.x));
if(result!=vyou.end())
vyou.erase(result);
a.x=b.x;
a.y=b.y+1;
if(a.y>n)
{
if(s.empty())
return 0;
else
huishu();
}
return 1;
}
bool isodd(int i)
{
if(i%2)
return true;
return false;
}
void out(int j,int k)
{
int i;
for(i=1;i<=n;++i)
{
if(i==k)
cout<<"皇";
else
{
if(isodd(j+i))
cout<<"□";
else
cout<<"■";
}
}
cout<<endl;
}
bool set_hh() //放置n皇后
{
a.x=1;
a.y=1;
do
{
if(try_hh(a)) //如果可以放置,则该点入栈
{
s.push(a);
vy.push_back(a.y);
vzuo.push_back((a.x+a.y));
vyou.push_back((a.y-a.x));
a.x+=1;
a.y=1;
}
else
{
if(a.y>=n)
{
if(!huishu())
return 0;
}
else
a.y+=1;
}
}while(a.x!=(n+1));
if(a.x=(n+1) && !s.empty())
{
while(!s.empty())
{
sok.push(s.top());
//cout<<s.top().x<<" "<<s.top().y<<endl;
//if((s.top()).x==1)
//s.pop();
s.pop();
}
while(!sok.empty())
{
out(sok.top().x,sok.top().y);
sok.pop();
}
//out((*it).x,(*it).y);
return 1;
}
else
return 0;
}
void init()
{
vy.clear();
vzuo.clear();
vyou.clear();
while(!s.empty()) s.pop();
while(!sok.empty()) sok.pop();
vy.push_back(0);
vzuo.push_back(0);
vyou.push_back(100);
}
int main(int argc,char* argv[])
{
while(true)
{
init();
cout<<"please putin n"<<endl;
cin>>n;
if(n==0)
break;
if(set_hh())
cout<<"success"<<endl;
else
cout<<"failure"<<endl;
}
return 0;
}
效果:

2、回溯法求八皇后的所有解
#include "stdio.h"
#include "math.h"
#define N0 8
int a[N0+1],b[N0+1]; //a存具体的行数b为有没标记
int c[17];//这个来标记对角线/的时候为行列值的和~16
int d[17];//这个来标记对角线\的时候相减为-7到不能用绝对值相减会少掉了一些值
//如(,1)和(,2)是可以但是就不能执行
int total=0;
void out()
{
char* str="皇";
char* qi1="□";
char* qi2="■";
int i,j;
for(i=1;i<=N0;i++)
{
for(j=1;j<=N0;j++)
if(a[i]==j) printf("%s",str);
else {
if((j%2==1&& i%2==1)||(i%2==0&&j%2==0)) printf("%s",qi1);
else printf("%s",qi2);
}
printf("\n");
}
printf("\n");
}
void try3(int k)
{
int i;
for(i=1;i<=N0;i++)
{
if(b[i]==0 && c[i+k]==0 && d[i-k+N0]==0)
{
a[k]=i;
b[i]=1;
c[i+k]=1;
d[i-k + 8]=1;
if(k==N0)
{
total++; //当为最后的时候也就是种数相加
printf("第%d种:\n",total);
out();
}else try3(k+1);
//以下为进行还原
b[i]=0;
c[i+k]=0;
d[i-k + N0]=0;
}
}
}
int main()
{
try3(1);
printf("total:%d\n",total);
return 0;
}
效果:

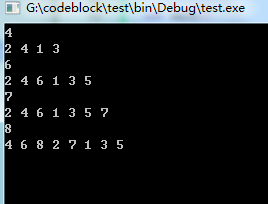
线性时间构造
1、线性时间构造n皇后的一个解,对n没有限制!
#include "stdio.h"
#include "stdlib.h"
int gs[10001];
int n;
int found;
int qmod(int r,int n)
{
return (2*r + n/2 - 3)%n;
}
/*
* works for even n when n%6 != 2
*
*/
void eq1()
{
int i;
for(i=1;i<=n/2;i++)
gs[i]=2*i;
for(i=n/2+1;i<=n;i++)
gs[i]=2*i-n-1;
}
/*
* works for even n when n%6 != 0
*
*/
void eq2()
{
int i;
for(i=1;i<=n/2;i++)
gs[i]=qmod(i,n)+1;
for(i=n/2+1;i<=n;i++)
gs[i]=n-qmod(n-i+1,n);
}
/*
* for odd n,we just put a queen at (n,n)
* then put the others as a n-1 queen problem
*/
void oq()
{
n--;
if (n%6 != 2)
eq1();
else
eq2();
gs[n+1]=n+1;
}
int main()
{
int i,j;
int oldn;
while(scanf("%d",&n) != EOF)
{
if(n==1)
{
printf("1\n");
continue;
}
if (n < 4)
{
printf("Impossible\n");
continue;
}
oldn=n;
if (n % 2 == 0 && n%6 != 2)
eq1();
else if (n%2 == 0)
eq2();
else
oq();
for(i=1;i<=oldn;i++)
printf("%d ",gs[i]);
printf("\n");
}
}
效果: